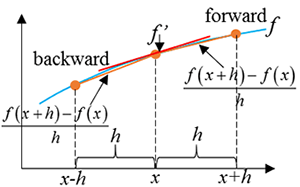
The Finite Difference Method (FDM) is an Eulerian method that involves approximating the derivative of a function using finite differences. It relies on a previously defined spatial discrete mesh of nodes. The starting point is the Newton-Raphson method, where the derivative of the function at a point equals the slope of the tangent line to the function (curve) at that point.
(more…)Category: Numerical Methods
Numerical Methods